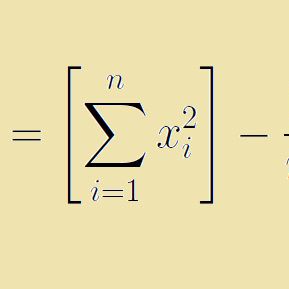In statistical data analysis the total sum of squares (TSS or SST) is a quantity that appears as part of a standard way of presenting results of such analyses. It is defined as being the sum, over all observations, of the squared differences of each observation from the overall mean.
Total Sum of Squares is defined and given by the following function:
Formula
Sum of Squares =∑(xi−x¯)2Sum of Squares =∑(xi−x¯)2
Where −
· xixi = frequency.
· x¯x¯ = mean.
Example
Problem Statement:
Calculate the sum of square of 9 children whose heights are 100,100,102,98,77,99,70,105,98 and whose means is 94.3.
Solution:
Given mean = 94.3. To find Sum of Squares:
| Calculation of Sum of Squares. | ||
| Column A Value or Score xixi | Column B Deviation Score ∑(xi−x¯)∑(xi−x¯) | Column C (Deviation Score)2(Deviation Score)2 ∑(xi−x¯)2∑(xi−x¯)2 |
| 100 | 100-94.3 = 5.7 | (5.7)2 = 32.49 |
| 100 | 100-94.3 = 5.7 | (5.7)2 = 32.49 |
| 102 | 102-94.3 = 7.7 | (7.7)2 = 59.29 |
| 98 | 98-94.3 = 3.7 | (3.7)2 = 13.69 |
| 77 | 77-94.3 = -17.3 | (-17.3)2 = 299.29 |
| 99 | 99-94.3 = 4.7 | (4.7)2 = 22.09 |
| 70 | 70-94.3 = -24.3 | (-24.3)2 = 590.49 |
| 105 | 105-94.3 = 10.7 | (10.7)2 = 114.49 |
| 98 | 98-94.3 = 3.7 | (3.7)2 = 3.69 |
| ∑xi=849∑xi=849 | ∑(xi−x¯)∑(xi−x¯) | ∑(xi−x¯)2∑(xi−x¯)2 |
| First Moment | Sum of Squares |