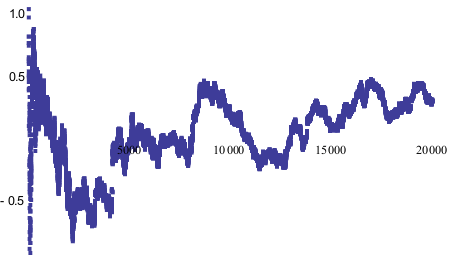
The weak law of large numbers is a result in probability theory also known as Bernoulli’s theorem. Let P be a sequence of independent and identically distributed random variables, each having a mean and standard deviation.

Formula

0=limn→∞P{|X−μ|>1n} =P{limn→∞{|X−μ|>1n}} =P{X≠μ}0=limn→∞P{|X−μ|>1n} =P{limn→∞{|X−μ|>1n}} =P{X≠μ}

Where −

·        nn = Number of samples

·        XX = Sample value

·        μμ = Sample mean

Example

Problem Statement:

A six sided die is rolled large number of times. Figure the sample mean of their values.

Solution:

Sample Mean Calculation

Sample Mean=1+2+3+4+5+66 =216,=3.5