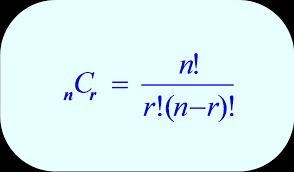A combination is a selection of all or part of a set of objects, without regard to the order in which objects are selected. For example, suppose we have a set of three letters: A, B, and C. we might ask how many ways we can select 2 letters from that set.

Combination is defined and given by the following function:

Formula

C(n,r)=n!r!(n−r)!C(n,r)=n!r!(n−r)!

Where −

·        nn = the number of objects to choose from.

·        rr = the number of objects selected.

Example

Problem Statement:

How many different groups of 10 students can a teacher select from her classroom of 15 students?

Solution:

Step 1: Determine whether the question pertains to permutations or combinations. Since changing the order of the selected students would not create a new group, this is a combinations problem.

Step 2: Determine n and r

n = 15 since the teacher is choosing from 15 students.

r = 10 since the teacher is selecting 10 students.

Step 3: Apply the formula

15C10=15!(15−10)!10!=15!5!10!=15(14)(13)(12)(11)(10!)5!10!=15(14)(13)(12)(11)5!=15(14)(13)(12)(11)5(4)(3)(2)(1)=(14)(13)(3)(11)(2)(1)=(7)(13)(3)(11)=3003