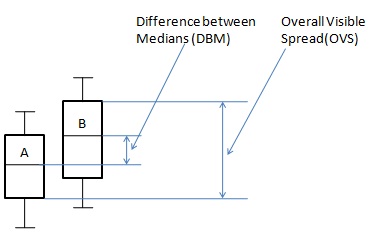
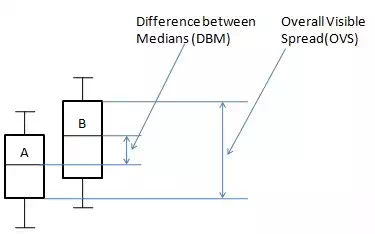
Groups of population can be compared using box and whisker plots. Overall visible spread and difference between median is used to draw conclusion that there tends to be a difference between two groups or not.

Case 2: Formula

P=DBMOVS×100P=DBMOVS×100

Where −

·        PP = percentage difference

·        DBMDBM = Difference Between Medians.

·        OVSOVS = Overall Visible Spread.

Rules

·        For a sample size of 30 if this percentage is greater than 33% there tends to be a difference between two groups.

·        For a sample size of 100 if this percentage is greater than 20% there tends to be a difference between two groups.

·        For a sample size of 1000 if this percentage is greater than 10% there tends to be a difference between two groups.

Example

Problem Statement:

Describe the difference between following sets of data.

Sr. No.	Name	Set A	Set B
1	Max	12	15
2	UQ	10	13
3	Median	7	10
4	LQ	6	9
5	Min	5	6

Solution:

Consider the following diagram:

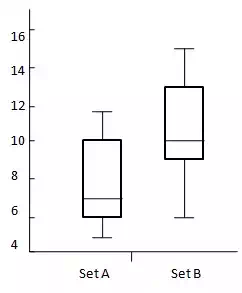
OVS=13−6 =7 DBM=10−3 =4OVS=13−6 =7 DBM=10−3 =4

Apply the formula

P=DBMOVS×100 =47×100 =57.14P=DBMOVS×100 =47×100 =57.14

As percentage is over 33% thus there is difference between Set A and Set B. It is likely that Set B is greater than Set A.