Quadratic regression is deployed to figure out an equation of the parabola which can best fit the given set of data. It is of following form:

y=ax2+bx+c where a≠0y=ax2+bx+c where a≠0

Least square method can be used to find out the Quadratic Regression Equation. In this method, we find out the value of a, b and c so that squared vertical distance between each given point (xi,yixi,yi) and the parabola equation (y=ax2+bx+2y=ax2+bx+2) is minimal. The matrix equation for the parabolic curve is given by:

⎡⎣⎢∑xi4∑xi3∑xi2∑xi3∑xi2∑xi∑xi2∑xin⎤⎦⎥⎡⎣⎢abc⎤⎦⎥=⎡⎣⎢∑xi2yi∑xiyi∑yi⎤⎦⎥[∑xi4∑xi3∑xi2∑xi3∑xi2∑xi∑xi2∑xin][abc]=[∑xi2yi∑xiyi∑yi]

Correlation Coefficient, r

Correlation coefficient, r determines how good a quardratic equation can fit the given data. If r is close to 1 then it is good fit. r can be computed by following formula.

r=1−SSESST where SSE=∑(yi−axi2−bx+i−c)2 SST=∑(yi−y¯)2r=1−SSESST where SSE=∑(yi−axi2−bx+i−c)2 SST=∑(yi−y¯)2

Generally, quadratic regression calculators are used to compute the quadratic regression equation.

Example

Problem Statement:

Compute the quadratic regression equation of following data. Check its best fitness.

x	-3	-2	-1	0	1	2	3
y	7.5	3	0.5	1	3	6	14

Solution:

Compute a quadratic regression on calculator by putting the x and y values. The best fit quadratic equation for above points comes as

y=1.1071×2+0.5714xy=1.1071×2+0.5714x

To check the best fitness, plot the graph.

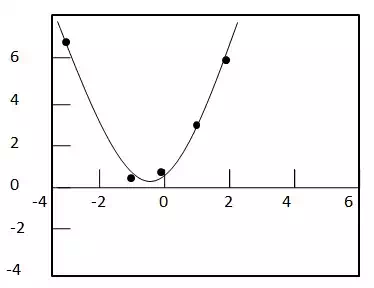
So the value of Correlation Coefficient, r for the data is 0.99420 and is close to 1. Hence quadratic regression equation is best fit.