The Rayleigh distribution is a distribution of continuous probability density function. It is named after the English Lord Rayleigh. This distribution is widely used for the following:

·        Communications – to model multiple paths of densely scattered signals while reaching a receiver.

·        Physical Sciences – to model wind speed, wave heights, sound or light radiation.

·        Engineering – to check the lifetime of an object depending upon its age.

·        Medical Imaging – to model noise variance in magnetic resonance imaging.

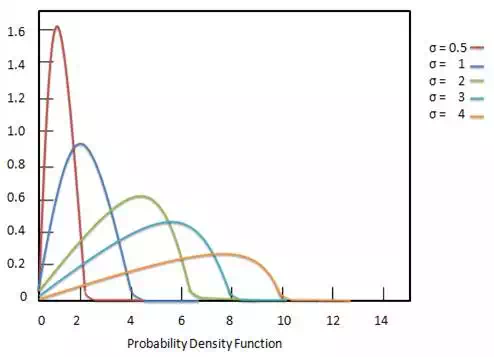
The probability density function Rayleigh distribution is defined as:

Formula

f(x;σ)=xσ2e−x22σ2,x≥0f(x;σ)=xσ2e−x22σ2,x≥0

Where −

·        σσ = scale parameter of the distribution.

The comulative distribution function Rayleigh distribution is defined as:

Formula

F(x;σ)=1−e−x22σ2,x∈[0∞F(x;σ)=1−e−x22σ2,x∈[0∞

Where −

·        σσ = scale parameter of the distribution.

Variance and Expected Value

The expected value or the mean of a Rayleigh distribution is given by:

E[x]=σπ2−−√E[x]=σπ2

The variance of a Rayleigh distribution is given by:

Var[x]=σ24−π2