Venn diagram is a way to visually represents relationship between groups of entities or objects. Venn diagrams are comprised of circles where each circle represents a whole set. Venn diagram can have unlimited circles but generally two or three circles are preferred otherwise the diagram becomes too complex.
Steps to draw a Venn Diagram
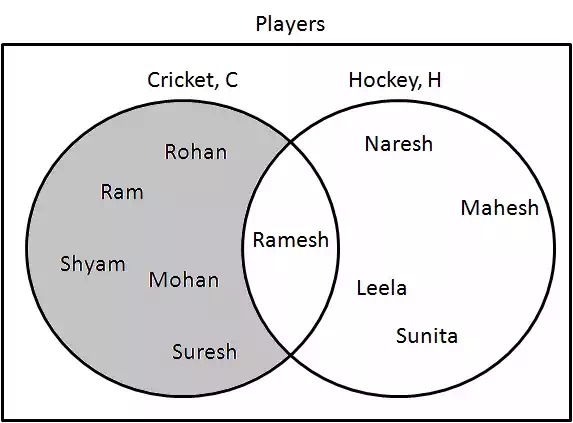
Consider the following sets of people:
1. Cricket Players – C={Ram,Shyam,Mohan,Rohan,Ramesh,Suresh}C={Ram,Shyam,Mohan,Rohan,Ramesh,Suresh}
1. Hockey Players – H={Ramesh,Naresh,Mahesh,Leela,Sunita}H={Ramesh,Naresh,Mahesh,Leela,Sunita}
Step 1: Draw a rectangle and label it as players.

Step 2: Draw two circles and label them as Cricket and Hockey. Make sure that circles are overlapping each other.

Step 3: Write Names inside the circle as relevant. Common name(s) should fall within common region.
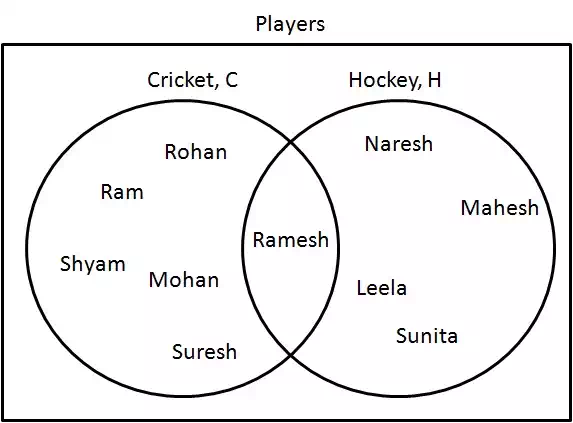
Union
Union (∪∪) represents a set where items are present in all categories but are not repeated.
Example
Problem Statement:
Draw a Venn diagram of C∪HC∪H.
Solution:
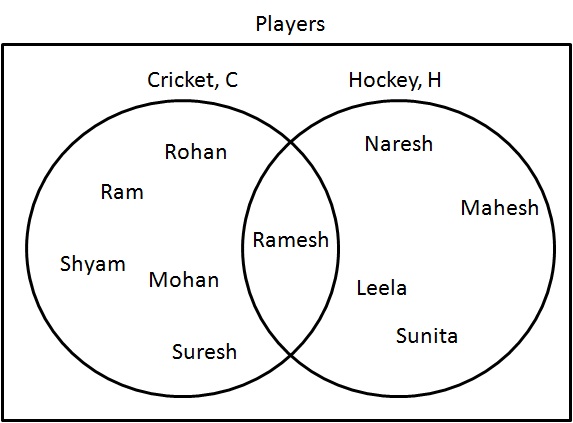
Step 1: Determine players who are either playing cricket or hockey. Draw them as following:
C∪H={Ram,Shyam,Mohan,Rohan,Ramesh,Suresh,Naresh,Mahesh,Leela,Sunita}C∪H={Ram,Shyam,Mohan,Rohan,Ramesh,Suresh,Naresh,Mahesh,Leela,Sunita}.
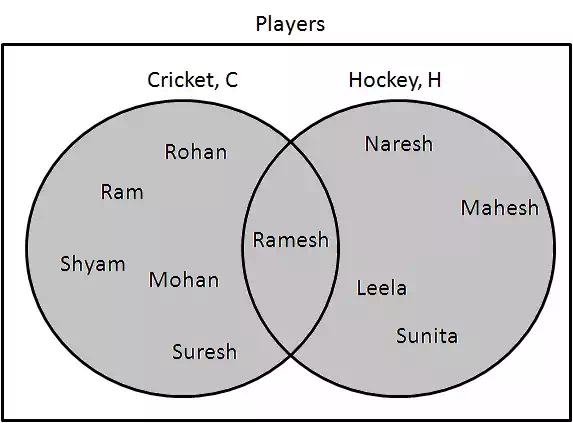
Intersection
Intersection (∩∩) represents a set where items are present in both categories.
Example
Problem Statement:
Draw a Venn diagram of C∩HC∩H.
Solution:
Step 1: Determine players who are playing cricket and hockey both. Draw them as following:
C∩H={Ramesh}C∩H={Ramesh}.
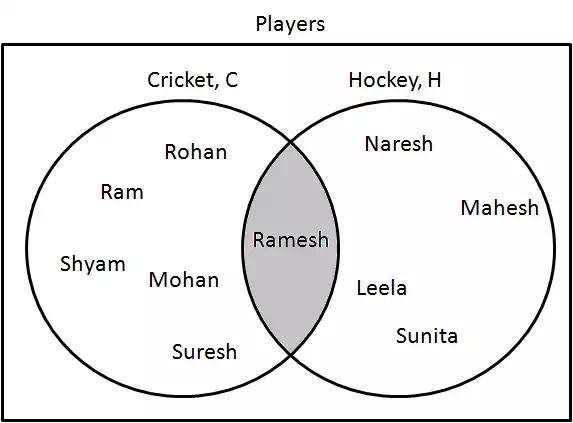
Difference
Difference (−−) represents a set where items are present only in one category and not in other one.
Example
Problem Statement:
Draw a Venn diagram of C−HC−H.
Solution:
Step 1: Determine players who are playing cricket only. Draw them as following:
C−H={Ram,Shyam,Mohan,Rohan,Suresh}C−H={Ram,Shyam,Mohan,Rohan,Suresh}.