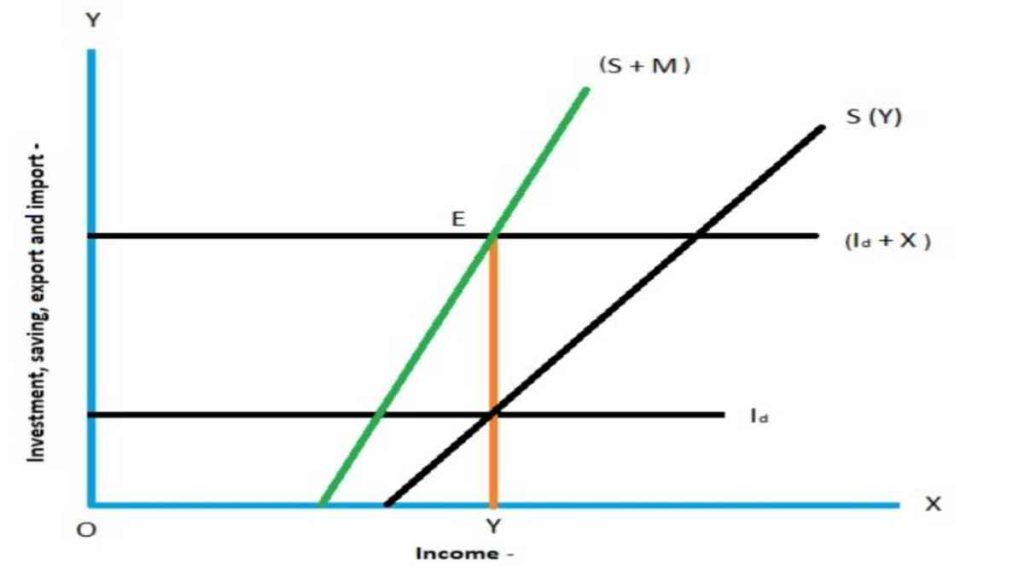
The foreign trade multiplier also known as the export multiplier operates like the investment multiplier of Keynes. It may be defined as the amount by which the national income of a nation will be raised by a unit increase in domestic investment on exports. As exports increase, there is an increase in the income of all persons associated with export industries. These in turn create demand for goods. But this is dependant upon their marginal propensity to save (MPS) and the marginal propensity to import (MPM). The smaller these two marginal propensities are, the larger will be the value of multiplier and vice versa.
Postulations
The foreign trade multiplier is based on the following:
There is full employment in the domestic economy
There is a direct link between domestic and foreign country in exporting and importing goods and the country is small with no foreign country
It is on a fixed exchange rate system The multiplier is based on instantaneous process without time lag and the domestic Investment (Id) remains invariable
There is no accelerator and the analysis is applicable to only two countries
There are no tariff barriers and exchange controls
The government expenditure is constant
Illustration 1
Let us assume the following:
MPS = 0.4
MPM = 0.4
Δ X = $ 2,000 millions
Where MPS is Marginal Propensity to Save and MPM is Marginal Propensity to Import. Calculate the foreign trade multiplier
Solution
The formula to calculate the foreign trade multiplier is
Kf = 1
MPS + MPM
Where,
MPS = Δ S and MPM = Δ M
Δ Y Δ Y
Δ Y = 1 Δ X
MPS + MPM
= 1 * 2,000
0.4 + 0.4
= 1 * 2,000
0.8
= 2,500
It shows that an increase in exports by $ 500 millions has raised national income though the foreign trade multiplier to $ 2,500 millions, given the values of MPS and MPM.
Illustration 2
An economy is characterised by the following equations:
Consumption C = 120 + 0.9Yd
Investment I = 20
Government G = 20
Expenditure
Tax T = 0
Exports X = 40
Imports M = 20 + 0.05 Y
What is the equilibrium income?
Calculate trade balance
What is the value of foreign trade multiplier?
Solution
1. National Income
Y = C + I + G + Nx
= 120 + 0.9Yd + 20 + 20 + 40 – (20 – 0.05Y)
= 120 + 0.9 (Y – T) + 20 + 20 + 40 – 20 – 0.05Y
= 120 + 0.9Y – 0 + 60 – 0.05Y
Y = 180 + 0.85Y
Y – 0.85Y = 180
0.15Y = 180
Y = 180 / 0.15
Y = 1,200
2. Trade Balance
X – M
= 40 – (20 + 0.05Y)
Substituting the value of Y, we have
Trade balance = 40 – [20 + 0.5(1,200)]
= 40 – 20 – 60
= – 40
Trade balance is in deficit.
3. Value of foreign trade multiplier = 1
1 – b + m
Where b is marginal propensity to consumer and m is marginal propensity to import.
Foreign Trade Multiplier = 1
1 – 0.9 + 0.05
= 1
0.15
= 6.67
Illustration 3
Behavioural and Structural equations of an economy are given below:
C = 200 + b (Y – 100 – tY)
I = 100
G = 100
X = 20
M = 10 + 0.1Y
The marginal propensity to consume ‘b’ is equal to 0.8 and proportional income tax rate, t = 0.25.
Find the equilibrium national income
Find foreign trade multiplier
Find equilibrium value of imports
If equilibrium national income falls short of full employment income by $ 100, how much government should increase its expenditure to attain full – employment?
Solution
1. Reduced form of the equation for equilibrium income is
Y = 1 (a – bT + I + G + X – Ḿ)
1 – b (1-t) + m
Substituting the values of the variables and parameters we have
Y = 1 (200 – (100*0.8) + 100 + 100 + 20 – 10)
1 – 0.8 (1-0.25) + 0.1
Y = 1 (330)
0.5
Y = 330 / 0.5
Y = 660
2. Foreign Trade Multiplier
= 1
1 – b (1-t) + m
= 1
1 – 0.8 (1-0.25) + 0.1
= 1 = 2
0.5
3. Equilibrium value of imports can be obtained by substituting the equilibrium income 660 in the import function. Thus
M = 10 + 0.1Y
M = 10 + 0.1(660)
M = 10 + 66 = 76
4. Required increase in Government expenditures to attain $ 100 increase in income can be obtained as under:
Δ Y = Foreign Trade Multiplier * Δ G
Δ Y = 2 * DG
Or Δ G = Δ Y = 100 = 50
2 2
Illustration 4
The equations in the economy are given as:
C = 400 + bYd
I = 140
Tax T = 120
Government = 140
Expenditure G
Exports X = 40
Imports M = 20 + 0.1Y
Marginal Propensity to consumer b = 0.8.
Find the equilibrium level of income
The value of the foreign trade multiplier
The equilibrium level of imports
Solution
The consumption function is
C = 400 + 0.8Yd
C = 400 + 0.8(Y – T)
C = 400 + 0.8(Y – 120)
The equilibrium condition is given as Y = C + I + G + X – M
Thus,
Y = 400 + 0.8(Y – 120) + 140 + 140 + 40 – 20 – 0.1Y
Y = 400 + 0.8Y – 96 + 140 + 140 + 40 – 20 – 0.1Y
Y = 604 + 0.7Y
Y – 0.7Y = 604
0.3Y = 604
Y = 604 /0.3
Thus equilibrium level of income is 2,013.33.
2. Foreign Trade Multiplier
Δ Y = 1
Δ X 1 – b + m
= 1
1 – 0.8 + 0.1
= 1 = 3.33
0.3
3. Imports at the equilibrium level
M = 20 + 0.1Y
= 20 + 0.1 (2,013.33)
= 20 + 201.333
= 221.333
The equilibrium level of imports is 221.333.