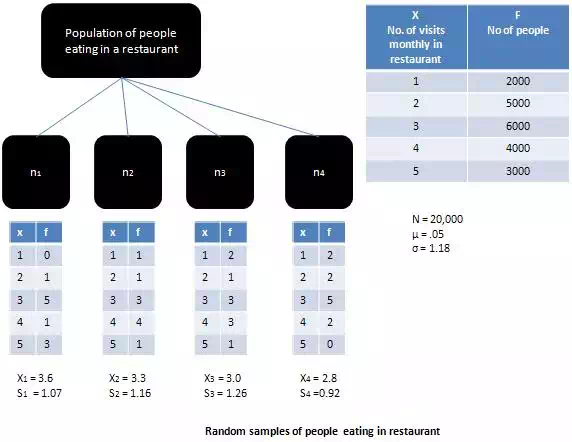
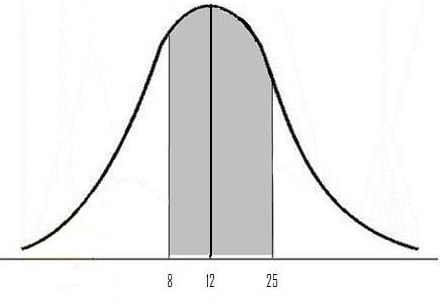
If the population from which the sample has a been drawn is a normal population then the sample means would be equal to population mean and the sampling distribution would be normal. When the more population is skewed, as is the case illustrated in Figure, then the sampling distribution would tend to move closer to the normal distribution, provided the sample is large (i.e. greater then 30).
According to Central Limit Theorem, for sufficiently large samples with size greater than 30, the shape of the sampling distribution will become more and more like a normal distribution, irrespective of the shape of the parent population. This theorem explains the relationship between the population distribution and sampling distribution. It highlights the fact that if there are large enough set of samples then the sampling distribution of mean approaches normal distribution. The importance of central limit theorem has been summed up by Richard. I. Levin in the following words:
The significance of the central limit theorem lies in the fact that it permits us to use sample statistics to make inferences about population parameters without knowing anything about the shape of the frequency distribution of that population other than what we can get from the sample.