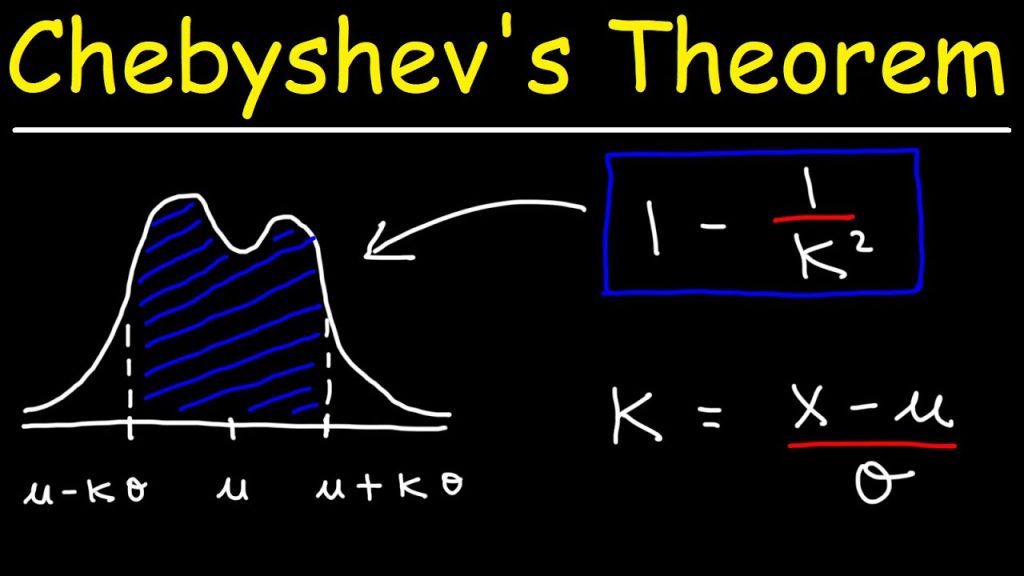
The fraction of any set of numbers lying within k standard deviations of those numbers of the mean of those numbers is at least

1−1k21−1k2

Where −

·        k=the within numberthe standard deviationk=the within numberthe standard deviation

and kk must be greater than 1

Example

Problem Statement:

Use Chebyshev’s theorem to find what percent of the values will fall between 123 and 179 for a data set with mean of 151 and standard deviation of 14.

Solution:

·        We subtract 151-123 and get 28, which tells us that 123 is 28 units below the mean.

·        We subtract 179-151 and also get 28, which tells us that 151 is 28 units above the mean.

·        Those two together tell us that the values between 123 and 179 are all within 28 units of the mean. Therefore the “within number” is 28.

·        So we find the number of standard deviations, k, which the “within number”, 28, amounts to by dividing it by the standard deviation:

k=the within numberthe standard deviation=2814=2k=the within numberthe standard deviation=2814=2

So now we know that the values between 123 and 179 are all within 28 units of the mean, which is the same as within k=2 standard deviations of the mean. Now, since k > 1 we can use Chebyshev’s formula to find the fraction of the data that are within k=2 standard deviations of the mean. Substituting k=2 we have:

1−1k2=1−122=1−14=341−1k2=1−122=1−14=34

So 3434 of the data lie between 123 and 179. And since 34=7534=75% that implies that 75% of the data values are between 123 and 179.