The chi-squared distribution (chi-square or X2X2 – distribution) with degrees of freedom, k is the distribution of a sum of the squares of k independent standard normal random variables. It is one of the most widely used probability distributions in statistics. It is a special case of the gamma distribution.

Chi-squared distribution is widely used by statisticians to compute the following:

·        Estimation of Confidence interval for a population standard deviation of a normal distribution using a sample standard deviation.

·        To check independence of two criteria of classification of multiple qualitative variables.

·        To check the relationships between categorical variables.

·        To study the sample variance where the underlying distribution is normal.

·        To test deviations of differences between expected and observed frequencies.

·        To conduct a The chi-square test (a goodness of fit test).

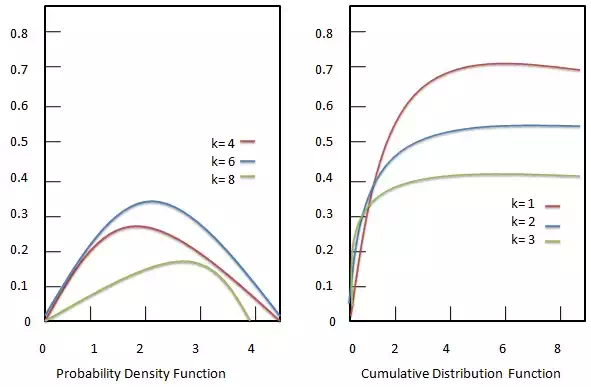
Probability density function

Probability density function of Chi-Square distribution is given as:

Formula

f(x;k)=f(x;k)= ⎧⎩⎨⎪⎪⎪⎪xk2−1e−x22k2Γ(k2),0,if x>0if x≤0{xk2−1e−x22k2Γ(k2),if x>00,if x≤0

Where −

·        Γ(k2)Γ(k2) = Gamma function having closed form values for integer parameter k.

·        xx = random variable.

·        kk = integer parameter.

Cumulative distribution function

Cumulative distribution function of Chi-Square distribution is given as:

Formula

F(x;k)=γ(x2,k2)Γ(k2)=P(x2,k2)F(x;k)=γ(x2,k2)Γ(k2)=P(x2,k2)

Where −

·        γ(s,t)γ(s,t) = lower incomplete gamma function.

·        P(s,t)P(s,t) = regularized gamma function.

·        xx = random variable.

·        kk = integer parameter.