Introduction to System Dynamics

Dr. Jay W. Forrester at the Massachusetts Institute of Technology created System Dynamics in the 1960s. It is a method for modelling and understanding the dynamic behavior of complex systems. Originally applied to the study of management and engineering systems, this powerful approach has found its way into many other fields, which study complex systems such as social, urban, economic, and ecological systems, amongst others.

First, let us define the word system. My favourite definition comes from Russel Ackoff, a professor at the Wharton School, and a pioneer in the field of Systems Thinking. In “Towards a System of Systems Concepts” (Ackoff 1971), Ackoff presents perhaps the best attempt at defining the concept of system. It can be summed up in the following definition:

A system is a set of two or more elements, and satisfying the following conditions:

·         Each element can affect the behavior of the whole.

·         The way each element affects the whole depends on at least one other element – i.e. no element has an independent effect on the whole

·         If you take any groups/subsets of elements and arrange them in any fashion, form subgroups in any way at all, then the subgroups will have these two properties: (the parts are interconnected.)

·         Every subgroup can affect the behavior of the whole

·         The way each subgroup affects the whole depends on at least other subgroup (no subgroup can have an independent effect)

An oversimplified version of this would be: “A system is a whole which cannot be divided into independent parts.

If we study this definition carefully, it implies two things about systems that are extremely important for management:

1) The essential properties of any system are properties of the whole which none of its parts have. Therefore when a system is taken apart it loses its essential properties. E.g. if we disassemble a car, we no longer have a car but a collection of car parts.

2) No system is the sum of the behaviour of its parts; it is a product of their interactions. When a system is disassembled, not only does it lose its properties, but so do all of the parts. E.g. an engine moves a car, but alone it moves nothing.

Therefore, we cannot study the development process without considering the development team (one criticism of CMM is that it looks at individual programmers as replaceable parts.) We cannot study the development team without understanding the software they are developing. And so on…

System Dynamics allows us to model the structure of a system and all its “parts”, including the time-delayed relationships among its components. The underlying relationships and connections between the components of a system are called the structure of the system. The term dynamics refers to change over time. If something is dynamic, it is constantly changing. A dynamic system is therefore a system in which the variables interact to stimulate changes over time. The way in which the elements or variables composing a system vary over time is referred to as the behaviour of the system. (Martin 1997)

Central to System Dynamics is the concept of feedback loops, and the concepts of stock and flow (also referred to as level and rate). A stock is something that accumulates (or drains) over time. A rate describes the quantity per unit-time at which a stock accumulates (or drains). Feedback loops are the cause-and-effect chains in the system through which a change in one variable creates a circular feedback, ultimately affecting itself.

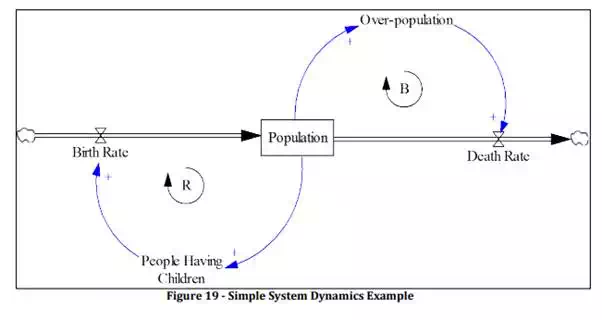
To demonstrate these concepts, Figure 19 presents a very simple example of a single stock system:

·         Population: is the stock that represents a human population.

·         Birth Rate and Death Rate are the rates at which the stock accumulates and drains, respectively.

·         The loop annotated with “R” is a positive feedback loop, also called a reinforcing feedback loop because it drives growth in the system. In our example: the more Population, the more People Having Children, and thus a higher Birth Rate, leading to even more Population. In other words, an increase in population triggers more increase in population.

·         The loop annotated with “B” is a negative feedback loop, also called a balancing feedback loop because it has a stabilizing effect on the system. In our example: the more Population, the greater Over-population, leading to a higher Death Rate, which causes a reduction in Population. In other words, an increase in population triggers a decrease in population.

The previous example is a very simple single-stock system with only two feedback loops. The study of a software development project on the other hand includes many stocks, variables, and loops. The type of large scale software projects we are interested in belong to the class of complex dynamic systems that, according to John Sterman (Sterman 1992), exhibit the following characteristics:

·         They are complex and consist of multiple components.

·         They are highly dynamic.

·         They involve multiple feedback processes.

·         They involve non-linear relationships.

·         They involve both “hard” and “soft” data.

In our case, hard data would be measurable data such as cost, and soft data would be more intangible data such as ‘employee motivation’.